A. 정의(Definition) 및 특성 (방향, 크기)
벡터(vector): 크기와 방향으로 정의되는 값, 속도, 위치이동, 힘 - 크기뿐만 아니라 방향까지 지정하지 않으면 완전히 표현할 수 없는 양, 벡터 는 크기와 방향을 갖는 유향선분 - 2차원, 3차원 공간의 벡터는 화살표로 표현 가능. 시작점과 끝점이 같아서 크기가 인 벡터를 영벡터라 한다(영벡터는 크기가 이므로 방향 은 임의 의 방향으로 한다).

이 외에 벡터에 대해 생각해볼 수 있는 정의는 '순서를 맞춰 숫자를 나열한 리스트라는 관점' 이라고도 볼 수 있다. (ex, 행렬식에서 벡터 (1,2,3) --> x = 1, y = 2, z = 3)
벡터 기본연산:
1). 벡터의 상수배(scalar multipliation):
어떠한 벡터가 있으면 이 벡터에 실수배를 함으로써 벡터의 크기가 늘었다 줄었다 한다.
밑의 화살표를 늘렸다 줄였다 하면서 생각해 보라.
그렇담 음의 실수배를 하면 어떻게 되겠는가?
그렇다 3사분면 방향으로 방향이 바뀔것이다.

2). 벡터 간의 합:
벡터들의 합은 밑의 그림을 기준으로 각 벡터의 x,y축 원소의 합으로 더하면 된다.

그렇담 뺄셈은 어떻게 하면 되나? x,y축 원소에 (-)를 곱해주어 더하면 된다!
위의 그림으로 설명하자면 만약 a벡터 - b벡터를 하고 싶으면 ,
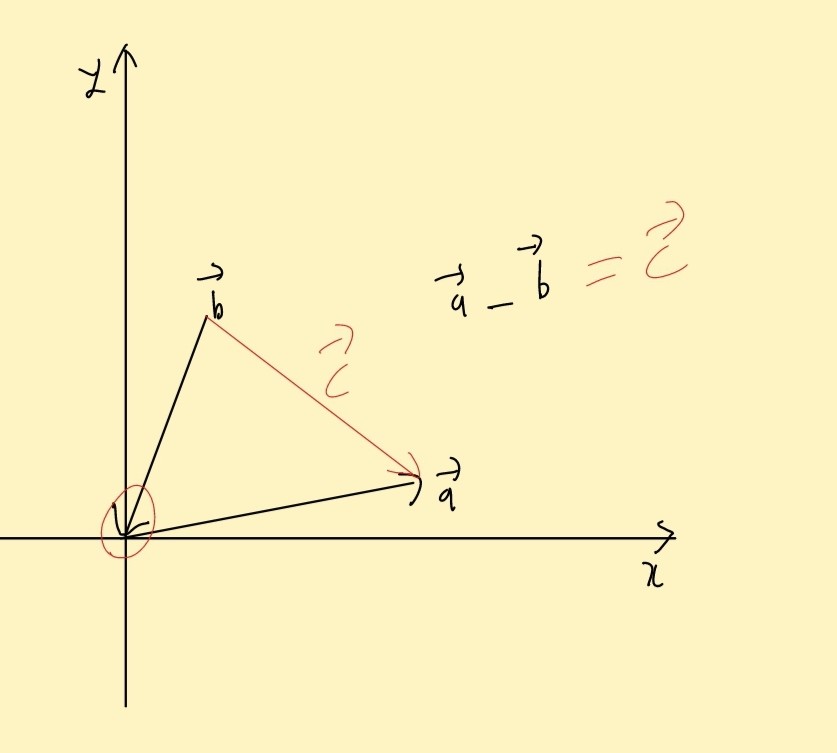
이런식이 된다.
참고로 수학에서의 벡터와 물리학에서의 벡터는 좀 의미가 다른데, 수학에서의 벡터는 모두 시점이 원점이어야 한다.
3). 벡터의 내적:
벡터의 내적은 쉽다.
벡터 x=(x1,x2,x3,) y=(y1,y2,y3)가 있으면
각원소들을 곱하고 합하면 된다.
모두가 알고 있듯이 벡터의 내적은 스칼라양이다. (고등학생 때 물리에서 배움)
내적에 관해서는 나중에 정사영 관련해서 좀더 다뤄 볼 예정이다.
내적은 그림자 라고 생각해 두면 좋다.
그 외 벡터의 성질들에 대해 간단히 설명해 보자면
4). 그 외 벡터들의 성질:
일단 벡터는
평면 벡터: x,y 두개의 순서조로 이루어져있는 벡터
공간벡터: x,y,z 세개의 순서조로 이루어져있는 벡터
다차원 벡터: x,y,z,...,n n개의 순서조로 이루어져있는벡터
들로 나눌 수 있는데
위 세 벡터는 차원만 다를 뿐 다른 벡터의 성질(벡터 곱, 스칼라배, 벡터 합 등)은 같다.
상등: 벡터의 원소들이 각각 같으면 상등이라고 한다.
영벡터: 시작점과 끝점이 같아서 크기가 인 벡터를 영벡터라 한다(영벡터는 크기가 이므로 방향 은 임의의 방향으로 한다).
다음에 추가작성.
'공부 > 선형대수학' 카테고리의 다른 글
| 1. 행렬(Matrix) (2) | 2023.05.10 |
|---|---|
| 1. 벡터(Vector) - (3, 정사영과 내적) (0) | 2023.05.04 |
| 1. 벡터(Vector) - (2) (0) | 2023.05.03 |